Hojas y páginas. Solución.

Enlace al problema

Los libros tienen las páginas impares en la primera cara de cada hoja y las páginas pares en la parte de atrás. Por tanto, el niño arrancó 4 hojas en total, ya que las páginas 127 y 128 están en la misma hoja.

Así que arrancó las páginas 5-6, 7-8, 53-54 y 127-128, es decir, 8 páginas.

Sudoku 6. Solución.

Sudoku 5. Solución.

Crucigrama sobre el clima y los ríos de España. Solución.

Enlace al crucigrama

SOLUCIÓN

Sudoku 3. Solución.

Sudoku 2. Solución.

En la zapatería. Solución.

Enlace al problema.
SOLUCIÓN.


El cliente intenta pagar pero como el dueño de la tienda no tiene cambio, lo consigue en la tienda de al lado. Cambia un billete de 10€ por dos de 5€.
 Da la vuelta de 5 € al cliente y se queda con 5€. Como ese era el mismo precio al que el dueño compró  las zapatillas, hasta ese momento no ganó nada pero tampoco perdió nada, sólo cubrió los gastos sin obtener beneficios.

Cuando le reclaman porque el billete de 10 € era falso, y tiene que dar otro billete de 10 €, es cuando se produce la pérdida de 10 €.

Saca la ficha. Solución.

Consecutivos separados. Solución.

Suma 15. Solución.

 

Cualquiera de las soluciones que habéis enviado son válidas, porque cumplen las mismas condiciones:

• En la casilla central ponemos el cinco
• A ambos lados de la casilla central (en todas las direcciones), tienen que ir grupos de números que sumen 10:

1 y 9

2 y 8

3 y 7

4 y 6

Por tanto habría otras maneras diferentes de colocar los números, como por ejemplo:

Seis copas. Solución.

Se coge la segunda copa empezando por la izquierda  y se vierte su contenido en la segunda copa empezando por la derecha.
Pulsa en la imagen para verlo.

Las seis copas

Acertio matemático 10. Solucion.

Enlace al problema.
SOLUCIÓN.
 El número 100 con nueve cifras idénticas se puede escribir así:
100 = 111-11+1-1+1-1
100 = 22x2x2+2+(2x2x2)+2
100 = 333:3-(3x3)-3+(3:3)
100 = 444:4-4-4-4+(4:4)
100 = 5x5x5-(5x5)+5-5+5-5
100 = 66+(6x6)-[(6+6):6x(6:6)]
100 = 7x7x (7+7):7+(7:7)+(7:7)
100 = 88+8+[8x8x8:8(8+8)]
100 = (99+99):(9+9)x9+(9:9)

Criptosuma 10. Solución.

Enlace al problema.
SOLUCIÓN







(criptosuma creada por Íñigo Tena, autor del blog: http://26veintiseis.blogspot.com/)

Multiplica 900. Solución.

Enlace al problema.
SOLUCIÓN.

Rellena los huecos. Solución.

Enlace al problema.
SOLUCIÓN.

Suma 9. Solución.

Enlace al problema.
SOLUCIÓN.

Cajas y balones. Solución.

Enlace al problema.

SOLUCIÓN.
En el problema no habla del tamaño de las cajas, así que, podemos usar cajas de diferentes tamaños. Hay varias posibilidades.
 
1º. Si usamos cajas de cuatro tamaños diferentes, de modo que unas encajen dentro de otras, podríamos resolverlo así:

• En la caja más pequeña guardamos un balón.

•  En la caja siguiente en tamaño, guardamos la caja más pequeña y dos balones más, por lo que en esa caja, habría un total de 3 balones.

• En la tercer caja, guardamos la caja anterior, y cuatro balones más, por lo que en su interior habrá un total de 7 balones.

• Por último, en la caja más grande, guardamos las otras 3 cajas anteriores y dos balones más, llegando a tener en su interior un total de 9 balones.

2º. Otra posibilidad sería utilizar una caja grande en la que cupieran otras 3 cajas, y dentro de esas 3, meteríamos 1, 3 y 5 balones respectivamente, sumando un total de 9 y cumpliéndose todas las condiciones.

Divide la tarta. Solución.

Enlace al problema

SOLUCIÓN.

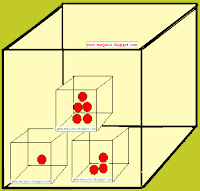
 Hay más de una opción. En el dibujo te muestro dos posibilidades:

1º. Considerando que no pudiéramos mover los trozos de la tarta, podríamos hacer dos cortes perpendiculares (en forma de cruz) pasando por el centro, y otro en sentido horizontal.

2º. Considerando que pudiéramos apilar los pedazos de tarta, podríamos dar un corte horizontal que la dividiera en dos bases iguales y otro corte vertical que la partiera a la mitad.

Apilaríamos después los 4 pedazos (en forma de media luna)

Por último, volveríamos a dar un corte vertical por la mitad para tener los 8 trozos iguales.

Criptosuma 9. Solución

 Solución.

121+212+888=1221

ROJO - 1
VERDE - 2
AZUL - 8


Criptosuma  creada por Íñigo Tena, autor del  blog: http://26veintiseis.blogspot.com/

Acertijos de Lenguaje. Solución.

Enlace a la entrada de los acertijos.

SOLUCIONES
1. ¿Qué palabra ( o palabras) de cuatro letras, si le quitas una queda una?
C-una
D-una
L-una
T-una
Una-s.

2. ¿Qué palabra tiene 5 sílabas y más de 20 letras?
Abecedario.

3. ¿A qué palabra (o palabras) de tres sílabas se puede quitar la sílaba del medio sin que pierda su significado? ( pista: numeral ordinal)
No(ve)no
No(ve)na.

Figuras mágicas (1 a 6). Solución

Enlace al problema

SOLUCIÓN

Cuántos hermanos y hermanas son. Solución.

Enlace del problema.

SOLUCIÓN
Siete en total.
Cuatro chicos y tres chicas.

Juego numérico 2. Solución.

Enlace al problema
SOLUCIÓN. Todos/as los/as que habéis enviado comentarios fueron respuestas diferentes y todas acertadas:
184+392=576
782+154=936
342+576=918
346+572=918

Hay bastantes más. Si alguien se anima aún está a tiempo.

Agua en el desierto. Solución.

Enlace al problema.
SOLUCIÓN.
Se llena totalmente el de 5 litros y se vierte en el de 3, quedando 2 litros en el de 5. Se vacía el de 3 y se pasan a éste los 2 litros que hay en el de 5, quedando 1 litro de capacidad libre en el de 3. Se llena de nuevo el de 5 y se vierte agua de éste en el de 3 hasta llenarlo, quedando así exactamente 4 litros en el recipiente de 5 litros.

Juego numérico 3. Solución.

Enlace al problema.

SOLUCIÓN.

Tod@s lo habeis resuelto muy bien. Destacaría la respuesta de Cristina Borge como modelo, porque ella además explica que una vez situado el número 5 en el medio, los demás pares de sumandos que sumen 10 ( 4 y 6; 7 y 3; 8 y 2;1 y 9) se pueden colocar donde quieras.

4+5+6
7+5+3
8+5+2
1+5+9

División del reloj.Solución.

Enlace al problema

SOLUCIÓN
El reloj debe dividirse para que sume lo mismo entre el 9 y el 10 y entre el 3 y el 4.
10+11+12+1+2+3 = 39
4+5+6+7+8+9 = 39

Padres e hijos en la isla. Solución.

Enlace al problema

SOLUCIÓN

Muy bien. Os fue fácil daros cuenta que el abuelo a la vez era padre y por eso había 3 personas, dos eran padres y dos eran hijos.

Mitad de dos mas tres. Solución.

Enlace del problema y de vuestras respuestas.
SOLUCIÓN
La mitad de dos es uno, y uno mas dos son tres.

La moneda diferente.Solución.

Enlace al problema.

SOLUCIÓN

Primero ponemos cuatro monedas en un platillo y otras cuatro en el otro. Pueden ocurrir dos cosas:
- o que la balanza se equilibre, en cuyo caso sabemos que la más pesada está entre las 4 que no hemos puesto en la balanza.
- o que la balanza se incline hacia un lado.
En el primer caso, cogemos las 4 monedas que no habíamos puesto en la balanza y pesamos 2 en cada platillo, vemos donde se inclina la balanza y repetimos la operación hasta encontrar la moneda más pesada.
En el segundo caso cogemos las 4 monedas del platillo hacia el que se inclinó la balanza y las dividimos de 2 en 2 para pesarlas de nuevo, vemos hacia donde se inclina la balanza y repetimos la operación hasta encontrar la moneda más pesada.

Culpables. Solución.

Enlace al problema.

SOLUCIÓN

Carlos y Bruno

Los tres dados. Solución.

Enlace al problema.
SOLUCIÓN
1º) O-M-E-F-U-V.
2º) S-G-C-I-T-Y.
3º) A-D-L-P-N-R.

Criptosuma 7. Solución.

Enlace a la criptosuma y a vuestras respuestas.



SOLUCIÓN.
28566
+7495
____
36061

Criptosuma 6

Enlace a la criptosuma y vuestras soluciones.

SOLUCIONES. Hay muchos resultados posibles. Algunos de ellos pueden ser:
523+ 523 +523 +523=2092
623+623+623+623=2492
723+723+723+723=2892

Seis unos. Solución

Enlace al problema.

SOLUCIÓN

Muy bien. Todas las respuestas enviadas fueron correctas:

1+1+11+11

Son 6 unos y 3 signos de sumar en una fila y el resultado es 24.

¿Quién es mayor?. Solución.

Enlace al problema.
SOLUCIÓN
Son mellizos y tienen 6 años.

Prueba:
6+2=8=2x4
6+3=9=3x3

Dentro de 2 años el niño será 2 veces mayor que era hace 2 años. Esta condición sólo se cumple si tiene actualmente 6 años, porque dentro de 2 años tendrá 8, y porque 8 es 2 veces más que 4, que es la edad que tenía hace 2 años (si ahora tiene 6).
La niña también tiene que tener 6 años, ya que dentro de 3 años tendrá 9, 3 veces mayor que era hace 3 años cuando tenía 3 (3x3).

Se busca. Solución.

Enlace al problema.

SOLUCIÓN

Efectivamente considerando el cero, el número buscado sería : 204862

Se cumplen todas las condiciones:
- Ninguna cifra es impar.Son: 0, 2, 4, 6 y 8
- La primera(centenas de millar) es un tercio de la quinta(decenas) y la mitad de la tercera(centenas). 2=6/3 y 2=4/2
- La segunda(decenas de millar) es la menor de todas, es decir, cero.
- La última (unidades) es la diferencia entre la cuarta(centenas) y la quinta(decenas).8 - 6 = 2
------------------------------------

Si no consideramos el cero, el número buscado al que habéis llegado much@s sería: 224862. Pero como vuestro razonamiento es estupendo, algun@s ya decíais que basándoos en la tercera condición que dice:
-" La segunda cifra(decenas de millar) es la menor de todas.",
sería muy discutible ese enunciado del problema y considerásteis que era inviable su resolución ya que si la 2ª cifra es igual a la primera, ya no sería "la" menor.

Enhorabuena. Me estáis dejando impresionada.