SOLUCIÓN.
En el problema no habla del tamaño de las cajas, así que, podemos usar cajas de diferentes tamaños. Hay varias posibilidades.
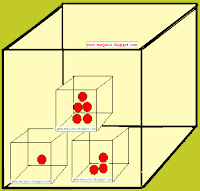
1º. Si usamos cajas de cuatro tamaños diferentes, de modo que unas encajen dentro de otras, podríamos resolverlo así:
- En la caja más pequeña guardamos un balón.
- En la caja siguiente en tamaño, guardamos la caja más pequeña y dos balones más, por lo que en esa caja, habría un total de 3 balones.

- En la tercer caja, guardamos la caja anterior, y cuatro balones más, por lo que en su interior habrá un total de 7 balones.
- Por último, en la caja más grande, guardamos las otras 3 cajas anteriores y dos balones más, llegando a tener en su interior un total de 9 balones.
2º. Otra posibilidad sería utilizar una caja grande en la que cupieran otras 3 cajas, y dentro de esas 3, meteríamos 1, 3 y 5 balones respectivamente, sumando un total de 9 y cumpliéndose todas las condiciones.





Pero mar Pelayo dijo que no valía meter una caja dentro de otra
ResponderEliminarNo es exactamente el problema que planteó Pelayo, porque después no me envió el enunciado, así que yo puse uno similar al que había sugerido, y si relees el enunciado que os redacté, yo no puse esa condición.
ResponderEliminarSi fuese como el problema de Pelayo, como sería la solución?
ResponderEliminarPelayo me habló en clase de un problema que consistía en meter 9 balones en 4 cajas con un número impar de balones en cada una, y ninguna ni vacía ni con la misma cantidad de balones. Como no recordaba bien todos el enunciado y después no me envió el problema exacto, publiqué uno que se ajustaba bastante a los datos que recordaba que me había dicho. Si Pelayo nos propone otro enunciado, lo podemos volver a resolver con otros datos que él nos dé.
ResponderEliminarami me apraece bueno
ResponderEliminar